Informace o studiu
Navazující Magisterské studium je sdružené studium dvou studijních programů maior/minor se standardní délkou studia 2 roky. Magisterské studium je ukončeno státní závěrečnou zkouškou, jejíž součástí je obhajoba diplomové práce. Absolventům magisterského studia se vydává diplom a dodatek k diplomu, tzv. Diploma supplement (v anglickém jazyce) a je jim přiznáván akademický titul „magistr“ (ve zkratce Mgr. uváděné před jménem).
V bakalářských, magisterských i doktorských studijních programech je uplatňován kreditový systém ECTS.
Na Katedře matematiky Pedagogické fakulty Univerzity Palackého v Olomouci můžete studovat navazující magisterský studiní program:
Učitelství matematiky pro 2. stupeň základních škol
(Mgr., 2 roky studia, sdružené studium maior/minor, prezenční nebo kombinovaná forma)
Charakteristika studijního programu
Navazující magisterský studijní program je určen především absolventům bakalářského studijního programu Matematika se zaměřením na vzdělávání, není ale uzavřen ani absolventům obdobného bakalářského studijního programu z jiných fakult a vysokých škol. Pro případné doplnění nezbytných znalostí z disciplín, jež jsou potřebné pro učitelství matematiky a budou součástí státní závěrečné zkoušky, je poskytnuta široká studijní nabídka povinných a povinně volitelných předmětů.
Absolvent si osvojí odborné i didaktické kompetence, které jsou předpokladem efektivního pedagogického působení (s důrazem na psychodidaktické kompetence, komunikační dovednosti, kooperaci a výchovu k samostatnému myšlení, jednání a potřebě dalšího vzdělávání a sebevzdělávání v oboru), ale umožňují také pokračovat ve vysokoškolském vzdělávání v doktorském studijním programu.
Studenti v průběhu studia prohlubují ucelený soubor poznatků ze základů matematiky jako vědy (teorie množin, statistika, vybrané kapitoly z moderních matematických disciplín, didaktické aplikace informačních technologií). Osvojují si poznatky a dovednosti z didaktiky matematiky, které aplikují v systému pedagogických praxí a jejich reflexí. Výuka uvedených disciplín je garantována katedrou matematiky. Kooperující katedry zabezpečující výuku předmětů pedagogicko – psychologického modulu společného základu.
Profil a uplatnění absolventa
Absolvent magisterského stupně získá odborné/teoretické znalosti z širšího spektra matematických disciplín, které jsou odborně předmětovým předpokladem jeho kvalitního pedagogického působení v nižším sekundárním školství. Má kvalitní vědomosti z didaktiky matematiky a dokáže je využít při vlastních vyučovacích činnostech jako součást reflexe absolvované pedagogické praxe. Je schopen samostatně a tvořivě využívat ICT při didaktických aplikacích matematického obsahu vzdělávání.
Dokáže získané poznatky tvořivě aplikovat ve svých vyučovacích postupech a výchovných činnostech. Používá analyticko-syntetické a induktivně-deduktivní myšlenkové postupy při řešení matematických úloh i v poznávacím procesu. Je seznámen s moderní didaktickou literaturou zaměřenou na jeho profesi a dokáže ji tvořivě aplikovat při inovaci svých učitelských kompetencí včetně zpracování a realizaci rámcového vzdělávacího programu. Je vybaven znalostí jednoho světového jazyka včetně základů cizojazyčné matematické terminologie.
Získá plnou kvalifikaci a profesní způsobilost pro výkon povolání učitele matematiky na 2. stupni základní školy.
Přijímací zkoušky
Nerealizují se. Předpokladem k přijetí ke studiu je úspěšné absolvování adekvátního bakalářského studijního programu.
Přijímací řízení
Ke studiu budou přijímáni absolventi bakalářského studijního programu Matematika se zaměřením na vzdělávání nebo absolventi obdobných bakalářských studijních programů z jiných fakult a vysokých škol.
Veškeré informace k přijímacímu řízení naleznete na stránkách Pedagogické fakulty v části pro uchazeče:
https://www.pdf.upol.cz/uchazec/prijimaci-rizeni-bakalarske-a-magisterske-studijni-programy/
Absolventi magisterských studijních programů, kteří získali titul Magistr, mohou vykonat v téže oblasti studia státní rigorózní zkoušku, jejíž součástí je obhajoba rigorózní práce. Po jejím vykonání se uděluje akademický titul PhDr. Podrobnosti níže.
Okruhy k SZZ
Studijní program: Učitelství matematiky pro 2. stupeň základních škol
Okruhy témat k Státní závěrečné zkoušce:
A) Vybrané okruhy odborných matematických problémů se zaměřením na souvislosti školské matematiky a integraci poznatků
- Základní pojmy teorie množin. Intuitivní teorie množin, Peanova množina, kardinální a ordinální čísla, mohutnost kontinua. Množiny ve školské matematice.
- Číselné obory a jejich rozšiřování. Motivace rozšíření, definice čísel celých, racionálních, reálných a komplexních. Dělitelnost v oboru celých čísel. Číselné soustavy. Reflexe ve školské matematice.
- Lineární rovnice a nerovnice, jejich soustavy. Algebraické a transcendentní rovnice. Diofantovské rovnice. Typy rovnic ve školské matematice, metody jejich řešení.
- Binární relace, zobrazení a funkce v matematice ZŠ. Vlastnosti, typy, příklady. Lineární, kvadratická funkce. Goniometrické funkce. Způsoby zadání funkce ve školské matematice.
- Základy kombinatoriky. Variace, permutace, kombinace. Užití v počtu pravděpodobnosti. Teorie grafů. Kombinační čísla a Pascalův trojúhelník ve školské matematice.
- Matematický pojem, definice, stavba a druhy definic. Axiomy, axiomatické systémy. Matematické věty a jejich důkazy. Formulování matematických vět ve školské matematice.
- Rovinné útvary, jejich klasifikace a zařazení do učiva ZŠ. Výpočty ploch rovinných útvarů pomocí integrálního počtu. Základní konvexní útvary v rovině (úsečka, polopřímka, polorovina, úhel, trojúhelník, rovinný pás).
- Základní pojmy stereometrie. Tělesa v učivu ZŠ. Zobrazovací metody (volné rovnoběžné promítání, pravoúhlá axonometrie, Mongeovo promítání). Základní konvexní útvary v prostoru (poloprostor, vrstva, klín, trojhran, trojboký hranolový prostor, čtyřstěn).
- Konstrukční úlohy v učivu matematiky na základní škole. Množiny bodů dané vlastnosti.
- Shodná zobrazení (Izometrie) v rovině. Podobná zobrazení (Podobnost) v rovině. Věty o podobnosti trojúhelníků.
B) Didaktika matematiky
Otázka z didaktiky matematiky má dvě části. V části b) řeší student úlohu z učiva matematiky základní školy, kterou si k danému tématu učiva vylosuje.
- a) Matematika jako komponenta kurikulárních dokumentů sekundární školy. Školská matematika v Rámcových vzdělávacích programech. Didaktická analýza učiva matematiky v sekundární škole.
b) Dělitel a násobek, prvočíslo, číslo složené, ciferný součet, Eratostenovo síto, znaky dělitelnosti, rozklad na prvočinitele, nejmenší společný násobek a největší společný dělitel čísel. Užití při řešení úloh typu: Určete největšího společného dělitele čísel 90 a 225. - a) Modernizace matematického vzdělávání. Základní trendy vývoje, zahraniční náměty a zkušenosti. Transmisivní a kontruktivistické přístupy k matematickému vzdělávání. Didaktická transformace matematických pojmů na základní škole.
b) Porovnávání čísel, poměr jednoduchý a postupný, rozšířit a krátit poměr, základní tvar poměru. Úměra a její výpočet. Kartézská soustava souřadnic, znázornění bodu a přímky v rovině. Přímá a nepřímá úměrnost (příklady). Graf přímé a nepřímé úměrnosti. Trojčlenka a její užití. Užití při řešení úloh typu: Adam, Bedřich a Cyril si mají rozdělit výhru 13 800 Kč tak, že Adam a Bedřich v poměru 3 : 4 a Adam a Cyril v poměru 2 : 3. Kolik Kč dostal každý? - a) Problematika motivace a kreativity v matematickém vyučování na jednotlivých stupních a typech škol. Zdroje, formy a nástroje motivace. Rozvíjení myšlení ve vyučování matematice.
b) Procento (promile), základ, procentová část, počet procent, grafické znázornění. Zavedení ve školské praxi. Způsoby výpočtu procentové části, počtu procent, základu. Využití v praxi. Užití při řešení úloh typu: Televizor byl zlevněn o 18 %, takže nyní stojí 10 250 Kč. Určete původní cenu. Znázorněte a řešte pomocí trojčlenky. - a) Komunikace v matematickém vyučování. Jazyk matematiky a jazyk školské matematiky. Terminologie a symbolika ve fylogenezi a ontogenezi.
b) Rovnost a rovnice, způsoby řešení lineárních rovnic o jedné neznámé, postup při řešení a diskuse. Lineární rovnice o dvou neznámých, geometrická aplikace a jejich řešení. Soustava dvou lineárních rovnic o dvou neznámých a jejich užití při řešení slovních úloh, geometrické aplikace. Kvadratická rovnice a její druhy a způsoby řešení. Lineární nerovnice a jejich řešení. Užití při řešení úloh typu: Řešte pro , proveďte zkoušku a určete podmínky řešitelnosti:
, proveďte zkoušku a určete podmínky řešitelnosti:
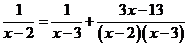
- a) Pracovní metody a postupy ve vyučování matematice. Indukce, dedukce, analogie, experiment, heuristika, algoritmus. Didaktické zásady v matematickém vyučování. Názornost, abstrakce a generalizace.
b) Výraz, číselné výrazy, výrazy s proměnnou, mnohočleny a operace s nimi. Základní algebraické vzorce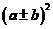 ,
, 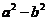 a jejich grafické znázornění. Lomené výrazy, smysl lomeného výrazu, rozšiřování a krácení lomených výrazů, operace s lomenými výrazy. Užití při řešení úloh typu: Vypočítejte a určete podmínky řešitelnosti:
a jejich grafické znázornění. Lomené výrazy, smysl lomeného výrazu, rozšiřování a krácení lomených výrazů, operace s lomenými výrazy. Užití při řešení úloh typu: Vypočítejte a určete podmínky řešitelnosti:
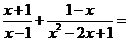
- a) Matematické učební úlohy, jejich místo v matematickém vzdělávání na různém stupni a typu školy. Didaktické funkce, typologie, metody řešení. Práce s matematickými učebními úlohami ve výuce jako reflexe odborných a didaktických kompetencí učitele.
b) Strany a úhly v pravoúhlém trojúhelníku, trojúhelníková nerovnost. Algebraická a geometrická definice Pythagorovy věty, věty obrácené, zobecněná Pythagorova věta. Užití Pythagorovy věty v planimetrii a stereometrii. Užití při řešení úloh typu: V pravoúhlém trojúhelníku ABC je součet délky odvěsny a přepony 19,2 cm a délka druhé odvěsny je 12,6 cm . Vypočítejte délky zbývajících stran. - a) Problematika evaluace v matematice. Měření pedagogických jevů, aplikace základních statistických pojmů v pedagogické teorii a školské praxi. Didaktické testy ve školské praxi. Chybný výkon žáka v matematickém vyučování, jeho analýza a interpretace.
b) Množiny bodů dané vlastnosti, konstrukční úlohy. Thaletova kružnice. Užití při řešení úloh typu: Sestrojte kružnici k, která se dotýká daných dvou rovnoběžek a,b a příčky p, která s přímkami a, b svírá úhel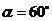 .
. - a) Didaktické prostředky pro vyučování matematice. Učebnice matematiky, její funkce a parametry. Informační a komunikační technologie v matematickém vzdělávání. Multimediální prostředky, interaktivní systémy a technologie v matematickém vzdělávání, aktuální software pro školskou matematiku.
b) Konstrukce trojúhelníků podle vět sss, sus, usu, Ssu (ssu). Konstrukce s využitím dalších prvků (výšky, těžnice, kružnice opsaná a vepsaná, úsekový úhel). Čtyřúhelníky, jejich rozdělení a základní konstrukce. Užití při řešení úloh typu: Sestrojte trojúhelník ABC, je-li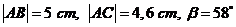 .
. - a) Základní etapy vývoje matematiky jako vědy. Periodizace. Směry vývoje v současné matematice. Historická poznámka v matematice ZŠ.
b) Základní tělesa (krychle, kvádr, hranol, válec, jehlan, kužel, koule). Jejich popis, vlastnosti, vzájemné vztahy a zobrazení ve školské praxi. Výpočet povrchu a objemu. Užití při řešení úloh typu: Kolik litrů vody je v nádobě tvaru kvádru o výšce 12 cm, je-li délka třikrát větší než šířka a výška je rovna polovině délky kvádru. - a) Matematické vzdělávání talentovaných a handicapovaných dětí. Péče o matematické talenty, matematické soutěže. Neprospěch v matematice. Poruchy učení a poruchy matematických schopností.
b) Podobnost geometrických útvarů, věty o podobnosti trojúhelníků, redukční úhel, změna a rozdělení v daném poměru. Užití podobnosti při odvození goniometrických funkcí ostrého úhlu na ZŠ Užití při řešení úloh typu: Změňte libovolný čtyřúhelník ABCD v poměru 3:2. (Použijte redukční úhel.)